 算法思想 - 优先遍历算法
算法思想 - 优先遍历算法
# 深度优先遍历
深度优先遍历(Depth First Search,简称 DFS)就是找准一条路不停深入的搜索方法,当发现这条路走不通的时候就会回退到上一个探索的节点,如果上一个节点存在没有探索的分支,便继续探索若没有则继续回退。深度优先遍历就有点像二叉树中的前序遍历、中序遍历和后序遍历。
它的特点是不撞南墙不回头,先走完一条路,再换一条路继续走。
深度优先遍历的关键就在于如何找到已经探索过节点的上一个节点,也就是如何回溯。
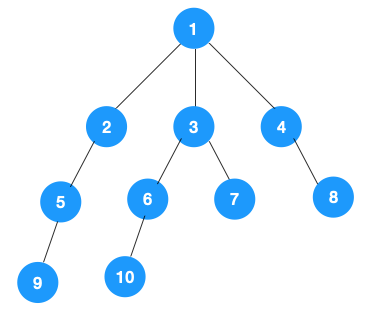
- 从根节点 1 开始遍历,它相邻的节点有 2,3,4,先遍历节点 2,再遍历 2 的子节点 5,然后再遍历 5 的子节点 9
- 此时 2 以及下面的节点遍历完后,回到根节点 1,继续遍历 3,6,10,7
- 此时 3 以及下面的节点遍历完后,回到根节点 1,继续遍历 4,8
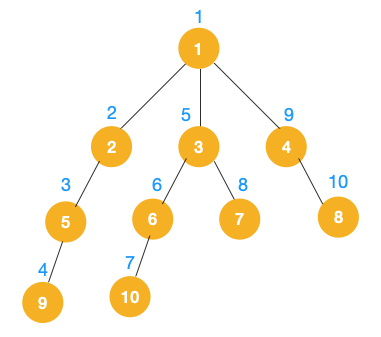
完整的遍历顺序图如下:
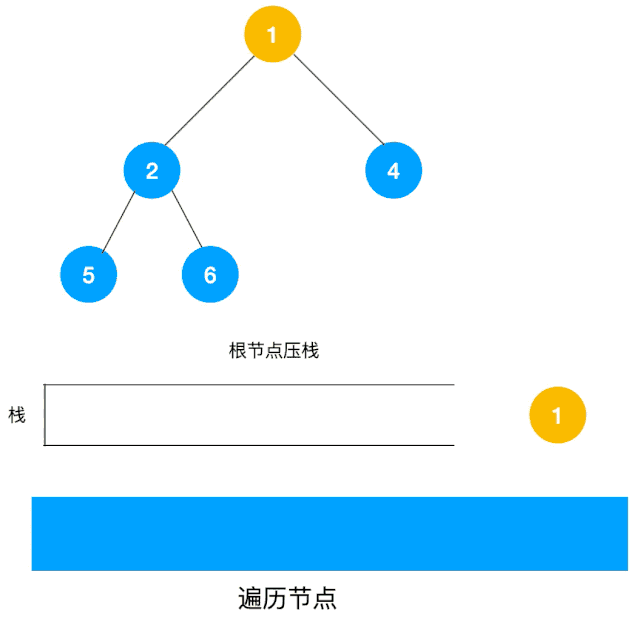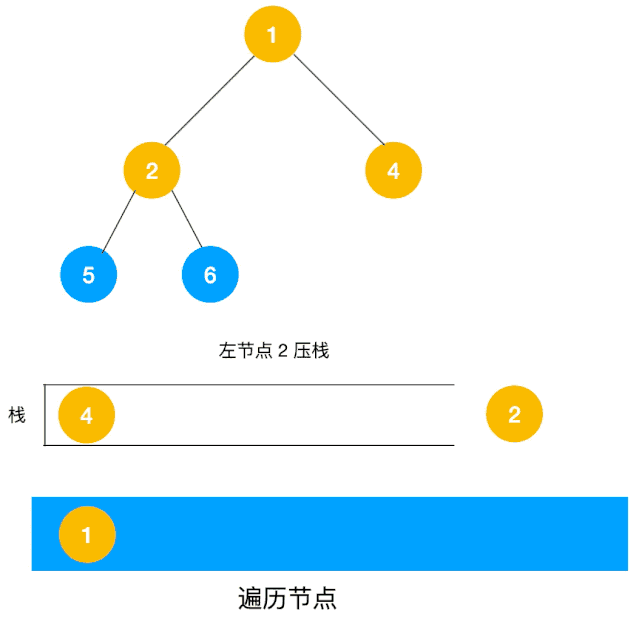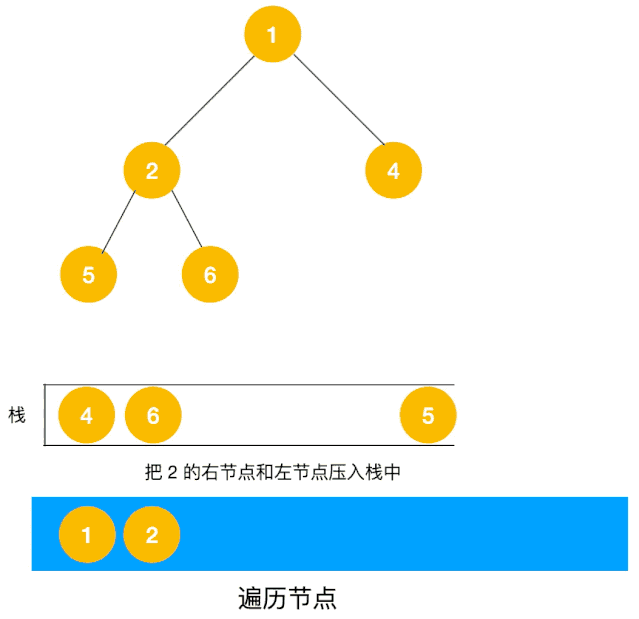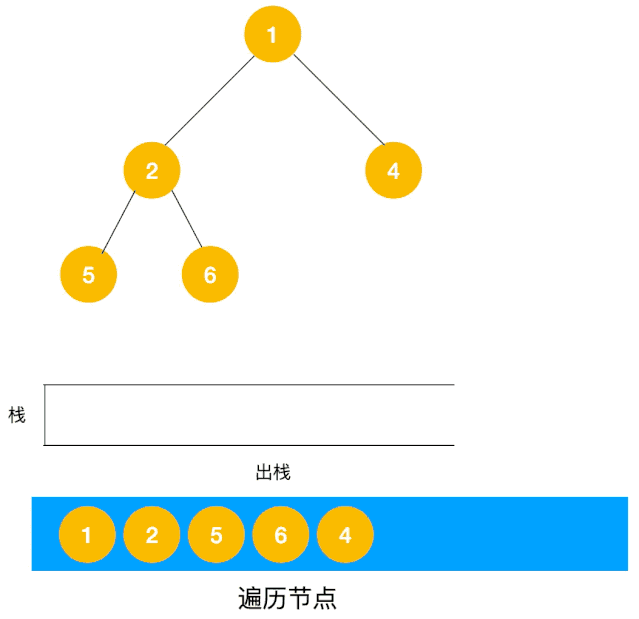
另一个利用栈的动图描述:
递归实现
public static void dfs(TreeNode root) {
if (root == null) {
return;
}
System.out.print("DFS 遍历,这里应该存节点,如:list.add(root)");
// 遍历左节点
preOrderRecur(root.left);
// 遍历右节点
preOrderRecur(root.right);
}
1
2
3
4
5
6
7
8
9
10
2
3
4
5
6
7
8
9
10
迭代实现
根据深度优先算法的特性,可以使用栈先入后出的特性实现。
将探索过的点存入栈内,遇到走不通的时候将栈顶元素出栈回到上一个元素,实现回溯
public static void dfs(TreeNode root) {
if (root == null) {
return;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
System.out.print("DFS 遍历,这里应该存节点,如:list.add(node)");
if (node.right != null) {
stack.push(node.right);
}
if (node.left != null) {
stack.push(node.left);
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
不难发现,上面的图这就是树的前序遍历,实际上不管是前序遍历,还是中序遍历,亦或是后序遍历,都属于深度优先遍历。
详细关于 DFS 的前序遍历、中序遍历、后序遍历的讲解,请看 算法模板 - 二叉树遍历。
# 广度优先遍历
广度优先遍历(Breath First Search,简称 BFS)一层一层遍历,每一层得到的所有新节点,要用队列存储起来以备下一层遍历的时候再遍历。
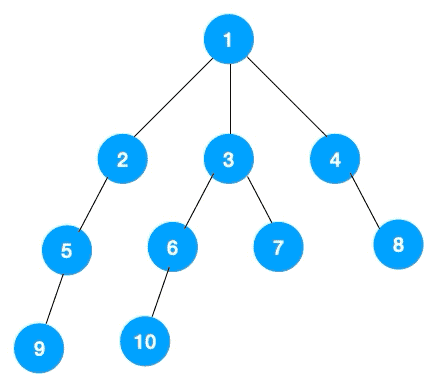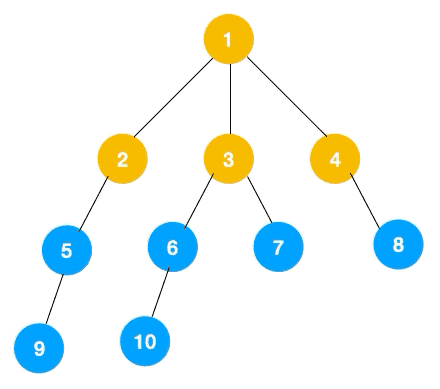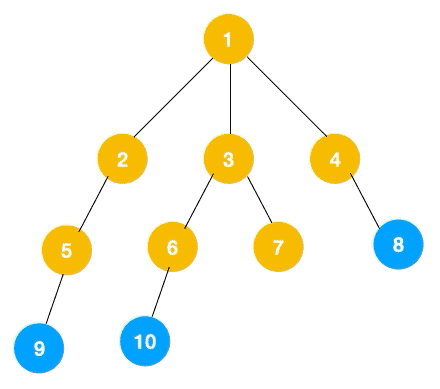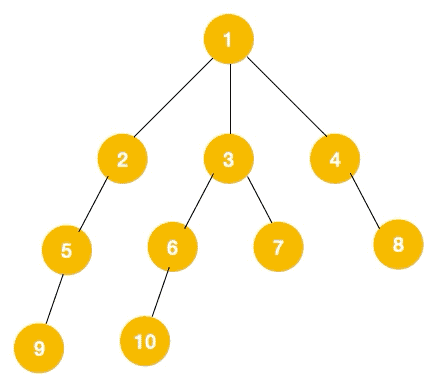
可以看出,遍历的顺序先是 2,3,4,接着是 5,6,7,8,最后是 9,10。属于一层一层遍历。
另一个利用队列的动图描述:
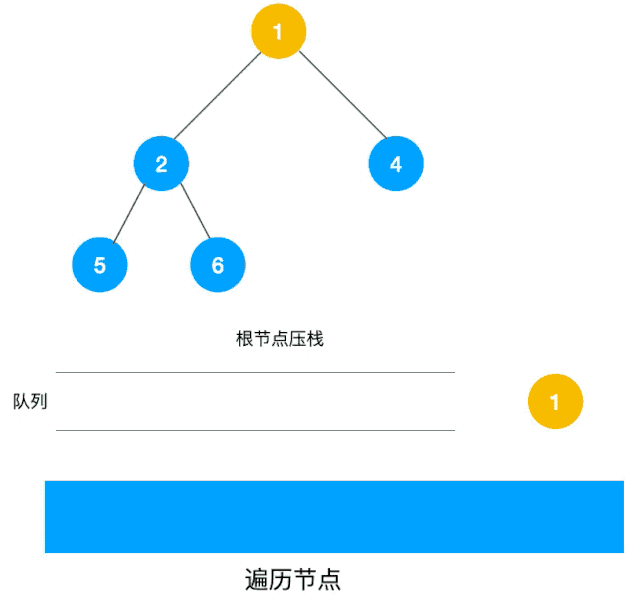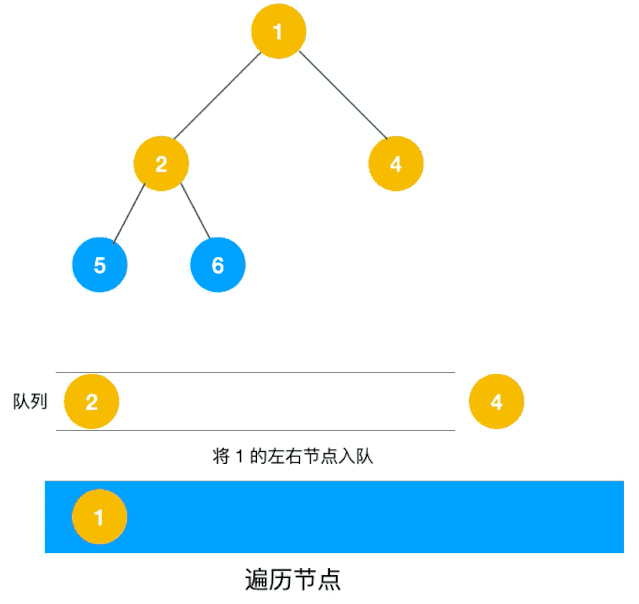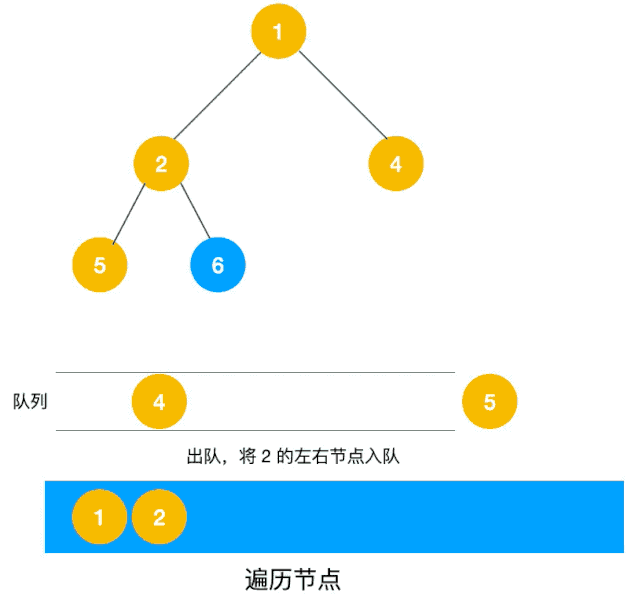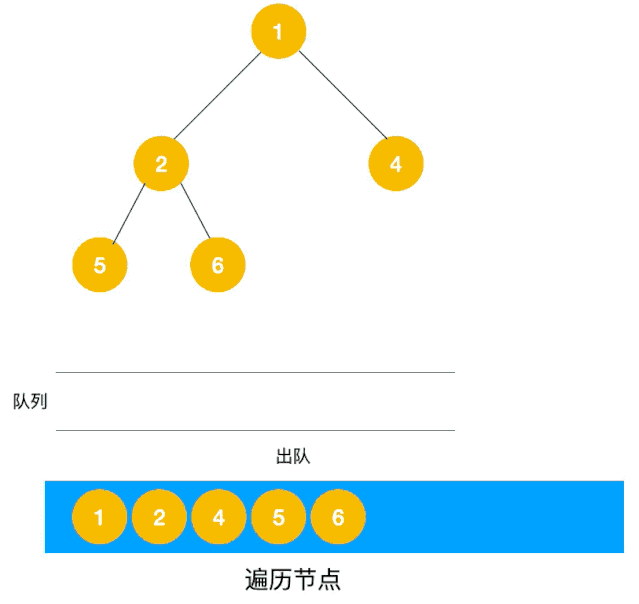
深度优先遍历用的是栈,而广度优先遍历要用队列来实现。
public static void bfs(Node root) {
if (root == null) {
return;
}
Queue<Node> queue = new LinkedList<>();
stack.add(root);
while (!queue.isEmpty()) {
Node node = queue.poll();
System.out.println("BFS 遍历,这里可以存节点,如 list.add(node)");
Node left = node.left;
if (left != null) {
queue.add(left);
}
Node right = node.right;
if (right != null) {
queue.add(right);
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
参考:https://developer.51cto.com/article/614590.html。
更新时间: 2024/01/17, 05:48:13
